Wie Berechnet Man Die Mantelfläche Eines Kegels
Netz und Oberflächeninhalt eines Kegels
Dice Oberfläche eines Kegels setzt sich zusammen aus:
- Grundfläche G: ein Kreis mit Radius r
- und Mantelfläche M: ergibt abgewickelt einen Kreissektor mit Kegelspitze als Mittelpunkt und Mantellinie southward als Radius. Die Bogenlänge b des Kreissektors ist genauso lang wie der Umfang des Grundflächenkreises (b = 2 π · r).
Der Oberflächeninhalt O eines Kegels ist:
O = G + G = π · r2 + π · r · s
Ein ii,v dm hoher Kegel hat eine Grundfläche, deren Durchmesser 16 cm beträgt. Berechne dice Oberfläche des Kegels.
Lösung:
Der gegebene Kegel sieht folgendermaßen aus (nicht maßstabsgetreu):
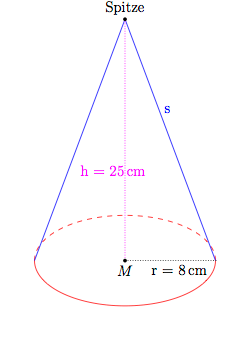
- Grundfläche
Die Grundfläche ist ein Kreis mit Radius 8 cm.
- Mantelfläche
In der Formel für den Mantelflächeninhalt taucht die Länge der Mantellinie south auf. Diese kann mithilfe des Satzes von Pythagoras aus dem gegebenen Radius und der Höhe berechnet werden:
Damit ergibt sich für die Mantelfläche:
- Oberfläche des Kegels
- Erklärung und Vertiefung
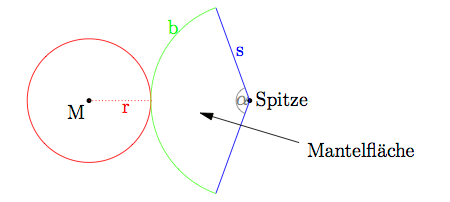
Die Mantelfläche ist abgewickelt ein Kreissektor mit Radius southward und Mittelpunktswinkel α. Die Länge der Mantellinie s kann - sofern sie nicht gegeben ist - mithilfe des Satzes von Pythagoras aus Radius und Höhe berechnet werden.
Der Mittelpunktswinkel α kann über die Bogenlänge b des Kreissektors ermittelt werden. Es golden:
| b | = |
|
und
| b | = |
|
Durch Gleichsetzen beider Formeln ergibt sich folgender Zusammenhang:
Für den Flächeninhalt der Mantelfläche ergibt sich damit die Formel:
| M | = |
|
Der Radius der Kegelgrundfläche ist 0,4 cm lang. Dice Länge der Mantellinie beträgt 12 mm. Berechne die Oberfläche des Kegels.
Lösung:
Der gegebene Kegel sieht folgendermaßen aus (nicht maßstabsgetreu):
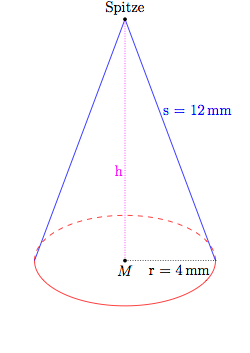
- Grundfläche
Die Grundfläche ist ein Kreis mit Radius four mm.
- Mantelfläche
- Oberfläche des Kegels
- Erklärung und Vertiefung

Die Mantelfläche ist ein Kreissektor mit Radius s und Mittelpunktswinkel α. Die Länge der Mantellinie s kann - sofern sie nicht gegeben ist - mithilfe des Satzes von Pythagoras aus Radius und Höhe berechnet werden.
Der Mittelpunktswinkel α kann über dice Bogenlänge b des Kreissektors ermittelt werden. Es aureate:
| b | = |
|
und
| b | = |
|
Durch Gleichsetzen beider Formeln ergibt sich folgender Zusammenhang:
Für den Flächeninhalt der Mantelfläche ergibt sich damit dice Formel:
| M | = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst!

Erfolgreich und motiviert lernen?
Jetzt unsere Online-Übungen ausprobieren!
- Keine Registrierung erforderlich!
- Aufgaben direkt im Browser bearbeiten und lösen.
- Für die Fächer Mathematik, Latein, Englisch, Chemie und Physik.
Zum Aufgabenbereich
Source: https://mathegym.de/mathe/wissen/739/beschreibe-das-netz-eines-kegels-und-gib-an-wie-man-seine-oberflaeche-insbesondere-mantelflaeche-berechnet

0 Response to "Wie Berechnet Man Die Mantelfläche Eines Kegels"
Post a Comment